प्रश्नावली-1B
1. निम्न में कौन सी संख्या अपरिमेय है?
(a) √ 36 = 6 परिमेय
64 8
(b) √3 अपरिमेय
(c) -9 = -9 परिमेय
√49 7
(d) √9 = 3 परिमेय
81 9
Answer:—- (b)
2. नीचे कयी समीकरण और कयी समुच्चय दिए गए हैं| प्रत्येक समीकरण का ठीक एक समुच्चय के साथ जोड़ा लगाएं ताकि समीकरण का हल उस समुच्चय में पाया जा सके—-
समीकरण
(i) 3x-9=2
(ii) x2-1=1
(iii) √2x=√8
(iv) x+95=59
जिस समुच्चय में है|
(a)प्राकृत संख्याओं का समुच्चय
(b)पूर्णांक का समुच्चय
(c)परिमेय संख्याओं का समुच्चय
(d)अपरिमेय संख्याओं का समुच्चय
Answer:—-
(i)<———–>(c)
(ii)<———–>(d)
(iii)<———–>(a)
(iv)<————>(b)
व्याख्यात्मक हल:—–
(i)3x-9=2 3x=9+2=11 x=11/3
(ii)x2-1=1 x2=1+1=2 x=√2
(iii)√2x=√8 x=√8/√2 x=4
(iv) x+95=59 x=59-95=-36
3. निम्नलिखित के केवल उत्तर लिखें-
(a)दो अपरिमेय संख्याओं के बीच कितनी अपरिमेय संख्याएँ होती है|
(b)दो वास्तविक संख्याओं के बीच कितनी वास्तविक संख्याएँ होती है|
(c)दो वास्तविक संख्याओं के बीच कितनी अपरिमेय संख्याएँ लिखी जा सकती है|
(d)परिमेय संख्याओं और अपरिमेय संख्याओं के समुच्चय में कितनी संख्याएँ उभयनिष्ठ है|
(e)परिमेय संख्याओं और अपरिमेय संख्याओं के सम्मुचय के सम्मिलन को कौन सा सम्मुचय कहा जाता है|
(f)क्या प्रत्येक अपरिमेय संख्या के संगत संख्या रेखा पर एक बिंदु होता है?
Answer:—–
(a)अनगिनत
(b)अनगिनत
(c)अनगिनत
(d)एक भी नहीं
(e)वास्तविक संख्याओं का समुच्चय
(f)हाँ
4. संख्या रेखा पर निम्नलिखित संख्याओं को प्रदर्शित करें-
(a)√3 (b)-√3 (c) 1 (d)√6
2 √6
Answer:—–
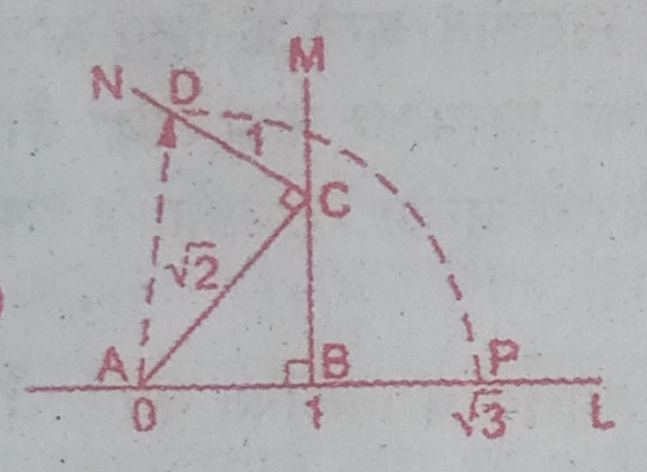
(a)
यहाँ AL संख्या रेखा है| AB=1, BC लंब AL, BC=1
तो AC कर्ण=√(ल०)2+(आ०)2
=√(1)2+(1)2=√2
पुनः CD लंब AC, CD=1
AD=√(AC)2+(CD)
= √(√2)2+(1)2=√3
पुनः AD=AP काटा बिंदु,
P, √3 को निरूपित करेगा|
(b)
| | | |
-√3 -√3 0 √3
2
(c)
यहाँ, AB=1, BC लंब AP, BC=1
AC=√(AB)2+(BC)2=
√(1)2+(1)2=√2
AP=AC काटा AP को Q पर समद्विभाजित किया| बिंदु Q 1 को निरूपित करता है|
√2
(d)
(√2)2=(1)2+(1)2
(√3)2=(√2)2+(1)2
(√5)2=(2)2+(1)2
(√6)2=(√5)2+(1)2








0 टिप्पणियाँ